스미스 차트(Smith Chart)는 주로 고주파 회로와 전자기학 분야에서 사용되는 그래프 도구입니다. 이 차트는 복소 임피던스와 반사 계수를 시각적으로 표현하는 데 매우 유용합니다. 스미스 차트는 원형 그래프로, 임피던스 또는 어드미턴스의 변화에 따라 그래프 위에서 위치를 표현할 수 있게 합니다. 다음은 스미스 차트의 주요 구성 요소와 사용 방법에 대한 설명입니다.
스미스 차트의 주요 구성 요소

- 임피던스 서클 (Impedance Circles):
- 차트의 수평 중심선은 실수 임피던스 (저항) 값에 해당하며, 수직 중심선은 허수 임피던스 (리액턴스) 값에 해당합니다.
- 동일한 실수 임피던스를 가지는 점들을 연결한 원들이 차트 위에 그려져 있습니다.
- 어드미턴스 서클 (Admittance Circles):
- 임피던스의 역수로서 어드미턴스 (컨덕턴스와 서셉턴스)가 표시됩니다.
- 어드미턴스는 스미스 차트에서 임피던스와 동일한 방식으로 원형 그래프로 표시됩니다.
- 반사 계수 (Reflection Coefficient):
- 스미스 차트는 반사 계수를 시각화하는 데 사용됩니다. 반사 계수는 복소 평면에서의 점으로 표현되며, 이를 통해 입력 임피던스를 계산할 수 있습니다.
스미스 차트의 사용 방법
- 임피던스 매칭:
- 주파수에 따라 변하는 임피던스를 매칭하기 위해 스미스 차트를 사용합니다. 임피던스 매칭은 전력 전달 효율을 극대화하는 데 중요합니다.
- 회로 분석:
- 스미스 차트를 사용하면 고주파 회로의 임피던스 변화를 쉽게 분석할 수 있습니다. 회로의 각 구성 요소가 임피던스에 미치는 영향을 시각적으로 파악할 수 있습니다.
- 전파 반사:
- 전송선로에서 발생하는 반사를 분석하는 데 사용됩니다. 반사 계수와 임피던스 변화를 시각적으로 표현하여 설계 및 분석 과정을 단순화합니다.
- 매칭 네트워크 설계:
- 안테나와 같은 고주파 장치에서 원하는 임피던스를 맞추기 위해 매칭 네트워크를 설계할 때 유용합니다.
스미스 차트의 장점
- 직관적 시각화: 복잡한 수식을 시각적으로 표현하여 이해하기 쉽습니다.
- 다양한 용도: 고주파 회로 설계, 임피던스 매칭, 전파 반사 분석 등 다양한 용도로 활용할 수 있습니다.
- 계산 단순화: 복소수 계산을 그래프를 통해 직관적으로 해결할 수 있습니다.
예시
스미스 차트를 통해 임피던스 매칭을 하는 예시는 다음과 같습니다.
- 주어진 임피던스를 스미스 차트에 표시합니다.
- 원하는 임피던스로 변환하기 위해 필요한 리액턴스나 저항값을 차트에서 읽어냅니다.
- 해당 값을 실제 회로에 적용하여 임피던스를 매칭합니다.
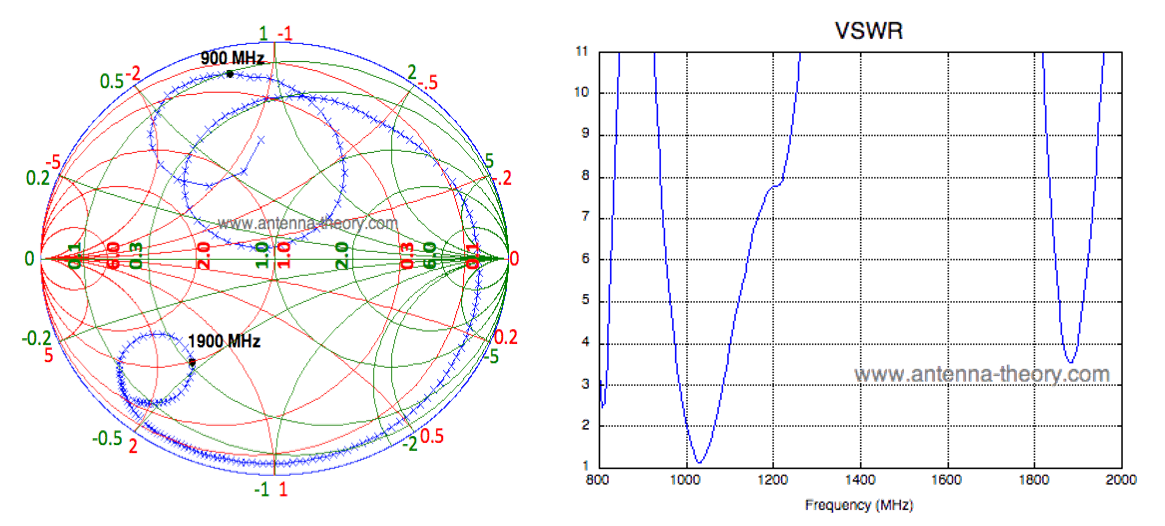
스미스 차트상 중앙에 가장 가까운 점에서 VSWR이 가장 낮은 것을 확인할 수 있다.
'플라즈마 및 전기전자공학 > 통신' 카테고리의 다른 글
| WR284, WR340, N, DIN 규격과 최대 Power (0) | 2024.06.14 |
|---|---|
| Circulator and Isolator (0) | 2024.06.14 |
| SPI 통신이란? (0) | 2024.06.10 |
| Master-Slave Network (0) | 2024.06.09 |
| EtherCAT이란? (0) | 2024.06.09 |
