Meow Engineering

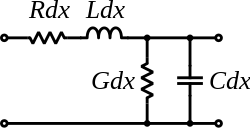
무손실 전송선로(Lossless Transmission Line)는 실제로 저항과 유전체 손실이 없는 이상적인 전송선로를 말합니다. 이 전송선로는 신호를 전송하는 동안 에너지를 잃지 않으며, 주로 고주파 신호를 전송할 때 사용되는 개념입니다. 무손실 전송선로의 특성과 주요 개념을 설명하겠습니다.

무손실 전송선로의 특성

무손실 전송선로에서는 저항($R$)과 컨덕턴스($G$)가 0으로 가정됩니다. 따라서 무손실 전송선로의 특성은 다음과 같이 요약될 수 있습니다:

• 저항( $R$ ) = 0
• 컨덕턴스( $G$ ) = 0

주요 파라미터

무손실 전송선로의 주요 파라미터는 다음과 같습니다:

1. 특성 임피던스 ($Z_0$​)

무손실 전송선로의 특성 임피던스는 다음과 같이 정의됩니다:

$Z_0=\sqrt{\frac{L}{C}}$

여기서,

• $L$: 단위 길이당 인덕턴스 (H/m)
• $C$: 단위 길이당 커패시턴스 (F/m)

이 특성 임피던스는 실수이며, 전송선로의 고유한 특성을 나타냅니다.

2. 전파 상수 ($\gamma$)

무손실 전송선로의 전파 상수는 복소수로, 다음과 같이 정의됩니다:

$\gamma =j\beta$

여기서,

• $\beta$: 위상 상수 (rad/m)

위상 상수 $\beta$는 다음과 같이 계산됩니다:

$\beta =\omega \sqrt{LC}$​

여기서 $\omega$는 각주파수 (rad/s)입니다.

전압과 전류의 분포

무손실 전송선로에서의 전압($V$)과 전류($I$)는 위치($z$)에 따라 다음과 같이 표현됩니다:

$V(z)=V_0^{+}{e}^{-j\beta z}+V_0^{-}{e}^{j\beta z}$

$I(z)=\frac{V_0^{+}}{Z_0}{e}^{-j\beta z}-\frac{V_0^{-}}{Z_0}{e}^{j\beta z}$

여기서 $V_0^{+}$​와 $V_0^{-}$는 각각 전송선로의 전진파와 반사파의 진폭을 나타냅니다.

반사와 정합

무손실 전송선로에서는 임피던스 정합이 매우 중요합니다. 전송선로의 특성 임피던스와 부하 임피던스가 일치하면 신호의 반사가 발생하지 않고, 최대 전력 전달이 이루어집니다. 임피던스 불일치가 발생하면 반사가 발생하여 신호 전송 효율이 떨어집니다.

이상적인 특성

무손실 전송선로는 에너지를 손실하지 않기 때문에 이상적인 전송선로로 간주되며, 다음과 같은 특성을 가집니다:

1. 에너지 손실 없음: 전송선로를 따라 신호가 전파되는 동안 에너지가 손실되지 않습니다.
2. 위상 변이: 신호의 진폭은 변하지 않고, 위상만 변합니다.
3. 주파수 독립성: 특성 임피던스는 주파수와 무관하게 일정합니다.

실제 응용

실제로 완벽한 무손실 전송선로는 존재하지 않지만, 이상적인 모델로 사용되어 전송선로의 설계와 분석에 중요한 기준을 제공합니다. 실제 전송선로에서는 저항과 유전체 손실이 있지만, 이를 최소화하려는 노력이 계속됩니다. 무손실 전송선로 모델은 마이크로파 회로, 안테나 시스템, 고속 데이터 통신 등에서 매우 유용합니다.

무손실 전송선로의 개념은 이론적 이해를 돕고, 실제 전송선로에서 발생하는 손실을 최소화하고 성능을 최적화하는 데 중요한 역할을 합니다.

손실 전송선로

손실 전송선로(Lossy Transmission Line)는 신호가 전송되는 동안 에너지가 손실되는 전송선로를 의미합니다. 이는 실제 전송선로에서 매우 일반적인 현상으로, 전송선로의 재료 특성과 구조로 인해 발생합니다. 손실 전송선로의 특성과 주요 개념들을 설명하겠습니다.

1. 손실의 종류

손실 전송선로에서 발생하는 손실은 주로 다음과 같은 두 가지로 나눌 수 있습니다.

a. 저항 손실(Conductor Loss)

전송선로의 도체(Conductor)가 저항을 가지고 있기 때문에 전류가 흐를 때 열로 에너지가 변환되어 손실이 발생합니다. 이는 전송선로의 길이, 도체의 재료, 단면적 등에 따라 달라집니다.

b. 유전체 손실(Dielectric Loss)

전송선로의 도체를 절연하는 유전체(Dialectric) 재료가 신호의 전송 과정에서 에너지를 흡수하여 열로 변환하는 현상입니다. 유전체의 재질, 주파수, 온도 등에 따라 달라집니다.

2. 전송선로의 파라미터

손실 전송선로의 성능을 나타내는 주요 파라미터는 다음과 같습니다.

a. 특성 임피던스(Characteristics Impedance, Z0Z_0Z0​)

전송선로의 고유한 임피던스로, 선로의 전기적 특성에 따라 결정됩니다. 이는 손실이 없는 전송선로와 동일하게 계산할 수 있습니다.

b. 감쇠 상수(Attenuation Constant, α\alphaα)

전송선로를 따라 신호의 크기가 감소하는 정도를 나타냅니다. 이는 저항 손실과 유전체 손실 모두를 포함한 값입니다.

c. 위상 상수(Phase Constant, β\betaβ)

전송선로를 따라 신호의 위상이 변하는 정도를 나타냅니다. 이는 주파수와 선로의 특성에 의해 결정됩니다.

3. 전송선로 방정식

손실 전송선로는 다음과 같은 복소수 파라미터로 나타낼 수 있습니다.

$\gamma =\alpha +j\beta$

여기서 $\gamma$는 전파 상수(Propagation Constant)로, 신호의 감쇠와 위상 변화를 모두 나타냅니다.

4. 전압과 전류 분포

손실 전송선로에서 전압과 전류는 다음과 같이 표현할 수 있습니다.

$V(z)=V_0^{+}{e}^{-\gamma z}+V_0^{-}{e}^{\gamma z}$ 

$I(z)=\frac{V_0^{+}}{Z_0}{e}^{-\gamma z}-\frac{V_0^{-}}{Z_0}{e}^{\gamma z}$

여기서, $V_0^{+}$와 $V_0^{-}$는 각각 전송선로의 전진파와 반사파의 진폭을 나타냅니다.

5. 중요성 및 적용 분야

손실 전송선로의 이해는 고주파 회로 설계, 통신 시스템, 마이크로파 및 RF 공학 등에서 매우 중요합니다. 실제로, 모든 전송선로는 어느 정도의 손실을 가지고 있기 때문에 이를 적절히 모델링하고 보상하는 것이 필요합니다.

손실 전송선로의 특성을 정확하게 파악함으로써, 신호 전달의 효율을 높이고, 시스템의 성능을 최적화할 수 있습니다.

손실 전송선로와 특성 임피던스

손실 전송선로와 특성 임피던스는 전송선로의 전기적 특성을 이해하는 데 중요한 관계를 가집니다. 특성 임피던스는 전송선로의 고유한 임피던스를 나타내며, 전송선로를 통해 전송되는 신호의 전압과 전류 간의 관계를 결정합니다. 손실 전송선로에서 특성 임피던스는 선로의 저항(R), 인덕턴스(L), 컨덕턴스(G), 및 커패시턴스(C)에 의해 결정됩니다.

손실 전송선로에서의 특성 임피던스

손실 전송선로의 경우, 특성 임피던스 $Z_0$​는 다음과 같은 복소수 형태로 표현됩니다.

$Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}$​​

여기서,

• $R$: 단위 길이당 저항 (Ω/m)
• $L$: 단위 길이당 인덕턴스 (H/m)
• $G$: 단위 길이당 컨덕턴스 (S/m)
• $C$: 단위 길이당 커패시턴스 (F/m)
• $\omega$: 각주파수 (rad/s)

손실이 없는 전송선로에서의 특성 임피던스

손실이 없는 전송선로에서는 $R=0$이고 $G=0$으로 가정할 수 있습니다. 이 경우 특성 임피던스는 보다 단순하게 다음과 같이 됩니다.

$Z_0=\sqrt{\frac{L}{C}}$​​

손실이 있는 경우와 없는 경우의 차이

손실이 있는 전송선로에서는 특성 임피던스가 복소수 값이 됩니다. 이는 전송선로에서 에너지가 손실됨을 의미하며, 주파수에 따라 변합니다. 반면에 손실이 없는 전송선로에서는 특성 임피던스가 실수 값이 되며, 이는 전송선로를 통해 신호가 손실 없이 전달됨을 나타냅니다.

물리적 의미

특성 임피던스는 전송선로의 입력 단자에 정합(impedance matching)이 잘 되었는지를 판단하는 중요한 기준입니다. 전송선로와 부하의 임피던스가 일치하면 신호 반사 없이 최대의 전력 전달이 가능합니다. 손실 전송선로의 경우, 복소수 특성 임피던스를 고려하여 정합을 맞추는 것이 중요합니다.

결론

손실 전송선로와 특성 임피던스는 전송선로의 성능과 효율성을 결정하는 중요한 요소입니다. 손실 전송선로에서는 저항 및 컨덕턴스로 인해 특성 임피던스가 복잡해지지만, 이를 통해 전송선로의 신호 전달 특성을 정확히 파악하고, 적절한 임피던스 정합을 통해 신호의 손실을 최소화할 수 있습니다.

※ ChatGPT-4o를 이용해 작성된 게시글입니다.

전송선 이론은 장거리 전도체를 통해 전기 신호가 전파되는 방식을 이해하는 데 필수적이며, 주로 통신, 전력 분배 및 고속 디지털 회로에 사용됩니다. 다음은 이 이론에 대한 포괄적인 설명입니다:

기본 개념

1. 전송선 기본:
   • 신호의 파장에 비해 회로가 매우 길어 전압 및 전류의 분포가 전송선 상에 위치에 따라서 다르게 나타납니다. 
   • 아래 그림이 전송선 이론의 개념을 잘 나타냅니다. 
   •  

     

2. 분포 파라미터:
   • 단순 회로가 집합된 파라미터(저항, 인덕턴스, 커패시턴스, 도전성)를 사용하는 것과 달리, 전송선은 분포 파라미터를 사용하여 분석됩니다.
   • 이 파라미터는 선의 길이에 따라 분포되며 다음을 포함합니다:
     • R (단위 길이당 저항): 도체의 저항으로 인한 전력 손실을 야기합니다.
     • L (단위 길이당 인덕턴스): 도체 주변에 형성된 자기장을 고려합니다.
     • C (단위 길이당 커패시턴스): 도체 간의 전기장을 나타냅니다.
     • G (단위 길이당 도전성): 절연 재료를 통해 도체 간에 누설 전류를 고려합니다.

     • 

3. 분포 파라미터: 이는 위치(z)와 시간(t)의 함수로서 전송선의 전압(V) 및 전류(I)를 설명하는 선형 미분 방정식 쌍입니다.

$$\frac{\partial V(z,t)}{\partial z}=-L\frac{\partial I(z,t)}{\partial t}-RI(z,t)$$

$$\frac{\partial I(z,t)}{\partial z}=-C\frac{\partial V(z,t)}{\partial t}-GV(z,t)$$

파동 전파

1. 특성 임피던스 (Z0):
   • 전송선의 중요한 특성으로, 다음과 같이 정의됩니다: $Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}$
   • 손실이 없는 선(R = 0, G = 0)의 경우 다음으로 단순화됩니다: $Z_0=\sqrt{\frac{L}{C}}$
   • 이는 선을 따라 이동하는 파의 전압과 전류 간의 관계를 결정합니다.
2. 전파 상수 (γ):
   • 신호가 전파되는 동안 감쇠 및 위상 변화를 설명합니다.
   $\gamma =\alpha +j\beta$
   • $\alpha$ 는 감쇠 상수(네퍼/미터)이고, $\beta$ 는 위상 상수(라디안/미터)입니다.

반사 및 전송

1. 임피던스 매칭:
   • 전송선이 부하에 종단될 때, 부하 임피던스 $Z_L$가 특성 임피던스 $Z_0$​와 일치하지 않으면 반사가 발생할 수 있습니다.
   • 반사 계수: $\mathrm{\Gamma }=\frac{Z_L-Z_0}{Z_L+Z_0}$​​
   • 완벽하게 매칭된 선($Z_L=Z_0$​)은 $\mathrm{\Gamma }=0$이며, 이는 반사가 없음을 의미합니다.
2. 정재파:
   • 입사파와 반사파의 중첩으로 인해 발생합니다.
   • 정재파비(SWR)는 불일치 정도를 나타냅니다:$SWR=\frac{1+|\mathrm{\Gamma }|}{1-|\mathrm{\Gamma }|}$​

실제 응용

1. 고주파 신호 전송:
   • 전송선은 신호 무결성이 중요한 RF(라디오 주파수) 응용 분야에서 중요합니다.
2. 디지털 회로:
   • 고속 디지털 회로에서 적절한 전송선 설계는 신호 열화 및 반사를 최소화하여 신호 무결성을 유지하는 데 필수적입니다.
3. 전력 분배:
   • 전력망의 전송선은 손실을 최소화하고 장거리 전기 에너지를 효율적으로 운반하도록 설계됩니다.

분석 기법

1. 스미스 차트:
   • 전송선 및 매칭 회로 문제를 해결하는 데 사용되는 그래픽 도구입니다.
   • 임피던스, 반사 계수 및 기타 파라미터를 시각화하는 데 도움이 됩니다.
2. 시뮬레이션 도구 (예: PSpice):
   • 복잡한 회로에서 전송선을 모델링하고 분석하는 데 사용됩니다.
   • 신호 동작을 예측하고 회로 성능을 최적화하는 데 도움이 됩니다.

결론

전송선 이론은 물리학, 수학 및 전기 공학 원리를 결합하여 신호가 도체를 따라 어떻게 전파되는지 이해합니다. 통신, 전력 분배 및 고속 전자 장치 시스템을 설계하고 분석하는 데 중요한 역할을 하며, 효율적이고 신뢰할 수 있는 신호 전송을 보장합니다.

특성 임피던스와 회로 임피던스의 차이

특성 임피던스 (Characteristic Impedance,$Z_0$​)

1. 정의:
   • 특성 임피던스는 무한히 긴 전송선의 고유한 속성으로, 전송선을 통해 전파되는 전압과 전류의 비율을 나타냅니다.
   • 수식으로 정의하면 다음과 같습니다: $Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}$​​
   • 여기서 $R$은 단위 길이당 저항, $L$은 단위 길이당 인덕턴스, $G$는 단위 길이당 도전성, $C$는 단위 길이당 커패시턴스입니다.
2. 특징:
   • 전송선의 특성에 따라 결정되며, 전송선의 물리적 구조와 재료에 의존합니다.
   • 신호가 반사 없이 전송되기 위해서는 부하 임피던스가 특성 임피던스와 일치해야 합니다.
3. 적용:
   • 고주파 신호가 전송선을 통해 이동할 때 중요합니다.
   • RF 회로, 안테나, 고속 디지털 신호 전송 등에 자주 사용됩니다.

회로 임피던스 (Circuit Impedance, $Z$)

1. 정의:
   • 회로 임피던스는 특정 지점에서 회로의 전압과 전류의 비율을 나타내는 일반적인 용어입니다.
   • 수식으로 정의하면 다음과 같습니다: $Z=\frac{V}{I}$​
   • 여기서 $V$는 전압, $I$는 전류입니다.
2. 특징:
   • 저항($R$), 인덕턴스($L$), 커패시턴스($C$)의 조합으로 구성됩니다.
   • 주파수에 따라 달라지며, 복소수 형태로 표현될 수 있습니다: $Z=R+jX$
   • 여기서 $R$은 저항, $X$는 리액턴스(인덕티브 리액턴스 또는 커패시티브 리액턴스)입니다.
3. 적용:
   • 회로의 임피던스를 이해하는 것은 회로 설계, 분석 및 신호 전송의 효율성을 최적화하는 데 필수적입니다.
   • 일반적인 전기 회로, AC 회로 분석 등에 사용됩니다.

주요 차이점

1. 적용 범위:
   • 특성 임피던스는 주로 전송선 이론에서 사용되며, 고주파 신호의 전송 특성을 설명합니다.
   • 회로 임피던스는 일반적인 회로 분석에서 사용되며, 다양한 회로 요소의 전압과 전류 관계를 설명합니다.
2. 구성 요소:
   • 특성 임피던스는 전송선의 물리적 특성과 재료에 의존하는 분포 파라미터($R$, $L$, $G$, $C$)를 포함합니다.
   • 회로 임피던스는 특정 지점의 저항, 인덕턴스 및 커패시턴스로 구성된 집중 파라미터를 포함합니다.
3. 반사 및 매칭:
   • 특성 임피던스는 전송선의 반사를 최소화하기 위해 부하 임피던스와 매칭되어야 합니다.
   • 회로 임피던스는 다양한 회로 구성 요소 간의 상호 작용을 분석하는 데 사용됩니다.

이와 같이, 특성 임피던스와 회로 임피던스는 각각 전송선과 일반 회로 분석에서 중요한 역할을 합니다. 두 개념을 이해하고 구분하는 것은 전기 및 전자 공학에서 필수적입니다.

※ ChatGPT-4o를 이용해 작성된 포스트입니다. 

※ 고양이 한마디: 특성 임피던스와 회로 임피던스는 이름이 같아 혼동을 주지만 완전히 다른 개념으로 기억해야 함.