Meow Engineering

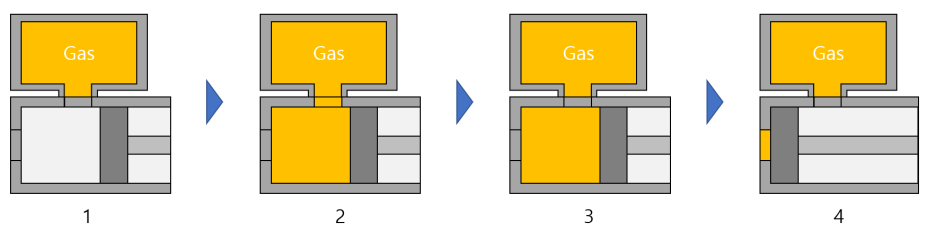
오늘은 디스크에 균일하게 입사하는 열에 의한 열응력을 계산해보고자 합니다. 

형상 및 가정

- 원형 디스크, 반지름 $R$

- 얇은 평판 → plane stress 조건

- 축대칭 (모든 물리량은 r에만 의존, $\theta$ 에 무관)

- 온도 분포: $T=T(r)$

- 재료는 선형 탄성, 등방성

- 구속 조건은 내부 응력만으로 평형을 이룬다고 가정 (즉, 외력 없이도 내부 응력 존재) 

1. 변형률 - 변위(Strain - Displacement) 관계

축대칭이므로, 변위는 반지름 방향으로만 존재하므로 u=u(r)이며, strain은 다음과 같다. 

$${ϵ}_r=du/dr,ϵ=u/r$$

$ϵ=u/r$ 은 원주방향 strain이기 때문에, 원주가 반경방향으로 팽창함에 따른 원주의 길이 증가를 생각하면 된다. 

단위 원주를 $L_0=r\cdot d\theta$ 이라고 할때, 축대칭 팽창하게 되면 이 단위 원주는 $L=(r+u(r))\cdot d\theta$가 되므로, 변형률은 $ϵ=(L-L_0)/L=u/r$이 된다. 

2. Stress-strain 관계

등방성재료에서 열팽창이 없는 경우의 일반적인 Hooke's law는 다음과 같다. 

$${\sigma }_r=\frac{E}{1-{\nu }^2}({ϵ}_r+\nu {ϵ}_{\theta })$$

$${\sigma }_{\theta }=\frac{E}{1-{\nu }^2}({ϵ}_{\theta }+\nu {ϵ}_r)$$

여기서 자유열팽창을 빼서 기계적 strain만을 고려하게 되면 다음과 같아진다. 

$${\sigma }_r=\frac{E}{1-{\nu }^2}({ϵ}_r+\nu {ϵ}_{\theta }-\alpha (1+\nu )T(r))$$

$${\sigma }_{\theta }=\frac{E}{1-{\nu }^2}({ϵ}_{\theta }+\nu {ϵ}_r-\alpha (1+\nu )T(r))$$

3. 요소에 대한 힘평형방정식

$$\frac{d{\sigma }_r}{dr}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0$$

$rd\theta ,dr,(r+dr)\theta$ 로 구성된 고리의 미소요소에 ${\sigma }_r(r),{\sigma }_{\theta },{\sigma }_r(r+dr)$을 넣고 힘평형 방정식을 세우면 구할 수 있다. 

4. 미분방정식 구성

$$\frac{d^{2}u}{d{r}^2}+\frac{1}{r}\frac{du}{dr}-\frac{u}{r^2}=\frac{(1+\nu )\alpha }{1-\nu }(\frac{dT}{dr}+\frac{\nu }{r}T)$$

u에 대해서 stress와 strain을 정리하며 구성하면 위 미분방정식을 얻을 수 있다. 

5. 미분방정식의 해

$${\sigma }_r(r)=\frac{E\alpha }{1-\nu }[\frac{1}{r}{\int }_0^{r}T(\rho )d\rho +\nu {\int }_r^R\frac{T(\rho )}{\rho }d\rho -T(r)]$$

$${\sigma }_{\theta }(r)=\frac{E\alpha }{1-\nu }[\frac{1}{r}{\int }_0^{r}T(\rho )d\rho +\nu {\int }_r^R\frac{T(\rho )}{\rho }d\rho -\nu T(r)]$$

예제: 균일 입사열 온도 구배에 따른 응력 분포

$$T(r)=T_0+\mathrm{\Delta }T(1-\frac{r^2}{R^2})$$

$${\sigma }_r(r)=\frac{E\alpha \mathrm{\Delta }T}{1-\nu }(\frac{1-2(r/R{)}^2}{4})$$

$${\sigma }_{\theta }(r)=\frac{E\alpha \mathrm{\Delta }T}{1-\nu }(\frac{1+2(r/R{)}^2}{4})$$

진공 챔버 내에서 가스를 제거하는 과정을 생각해 봅시다. 시간에 따라 가스를 제거할 때 다음과 같이 표현할 수 있습니다.

$$\frac{dm}{dt}$$​

여기서 mmm은 가스의 질량입니다. 가스의 질량을 밀도와 부피로 표현할 수도 있고, 분자량과 분자수로도 표현할 수 있습니다. 후자의 방법으로 표현해보겠습니다.

$$\frac{dm}{dt}=\frac{d(Nmi)}{dt}$$​

여기서 $m_i$ 는 분자량이고, $N$ 은 분자수입니다. 이상기체 상태방정식 $PV=NkT$를 이용하면 다음과 같이 정리할 수 있습니다.

$$\frac{dm}{dt}=\frac{d}{dt}(\frac{m_{i}PV}{kT}))$$

$m_i$, $k$는 상수이고, 진공 펌핑 과정에서 $T$ 를 상수로 가정할 수 있습니다. 이는 열교환기를 통해 상온으로 유지되기 때문입니다. 이를 이용하면 다음과 같이 정리할 수 있습니다.

$$\frac{dm}{dt}=\frac{m_i}{kT}\frac{d}{dt}\left(PV\right)=\frac{m_i}{kT}Q,Q=\frac{d}{dt}\left(PV\right)$$

Pumping Speed 개념을 이해하기 위해 피스톤 펌프의 작동 원리를 생각해봅시다. 피스톤 펌프는 다음 4가지 단계로 구분할 수 있습니다.

 

1. 측면 게이트를 닫고 피스톤을 원위치로 복귀시킵니다.
2. 상부 게이트를 열어 실린더 내로 기체를 받아들입니다.
3. 상부 게이트를 닫습니다.
4. 측면 게이트를 열고 피스톤을 움직여 실린더 내 가스를 배출합니다.

압력과 부피의 곱의 시간 변화율이 가스의 유량임을 알고 있습니다. 실린더 내로 들어온 가스의 압력과 부피의 곱을 구한 후 전체 행정에 걸리는 시간으로 나누면 펌프의 유량을 구할 수 있습니다.

$$Q=\frac{d}{dt}(P_{ch}\times V_{cylinder})=P_{ch}\times \frac{d{V}_{cylinder}}{dt}=P_{ch}S,S=\frac{d{V}_{cylinder}}{dt}$$

​

여기서 PchP_{ch}Pch​가 시간에 따라 불변한다고 가정합니다. 이는 챔버의 부피에 비해 실린더의 부피가 매우 작기 때문에 타당합니다. 따라서 챔버 압력과 실린더 부피 변화율의 곱으로 유량을 산출할 수 있습니다. 이를 배기 속도로 일반화할 수 있습니다. 정리하면 다음과 같습니다.

$$Q=SP$$

$S$ 는 배기 속도이고, $P$ 는 챔버의 압력입니다. $S$ 의 단위는 $\frac{L^3}{/}s$의 차원을 가집니다. 이는 나중에 얘기할 컨덕턴스의 단위와 같지만, 유도 과정과 의미는 다릅니다.

실 설비에서 위 공식이 적용되지 않는 상황들도 있습니다. 예를 들어, 이상기체에서 크게 벗어난 가스나, 펌프가 챔버의 압력을 한 번에 바꿀 수 있을 정도로 배기 속도가 큰 경우, 펌핑 속도가 시간에 따라 달라지는 상황 등이 있습니다.

※ 고양이가 직접 작성한 포스트입니다. 

크누센 수(Knudsen Number)는 평균자유거리와 배관 직경의 비율로 정의됩니다.

$$Kn=\lambda /d$$

여기서 $\lambda$는 평균자유거리이고, $d$는 배관 직경입니다. 배관 직경은 분자가 운동하는 공간의 특성을 나타내는 특성값으로, 공간의 형태에 따라 달라질 수 있습니다. 평균자유거리는 분자의 크기, 압력, 온도에 따라 변합니다.

Knudsen 수의 값에 따라 유동의 특성은 다음과 같이 나뉩니다:

점성류는 기체 분자간의 충돌이 지배적인 구간입니다. 유체 역학에서 다루는 대부분의 유체는 이 범주에 속합니다. 점성류에서는 기체 분자간 충돌이 지배적으로 작용하며, 벽과의 충돌은 경계 조건에 영향을 미칩니다. 기체 분자간 충돌이 지배적이라는 것은 유체를 연속체로 가정할 수 있다는 의미로, 유체의 일부분을 확대해도 같은 상태를 유지하기 때문에 미분방정식을 적용할 수 있습니다.

분자류에서는 기체 분자간 충돌이 거의 없고, 기체 분자와 벽간 충돌이 지배적입니다. 이 경우 기존 유체 역학의 미분 방정식을 사용할 수 없으며, 각 분자의 운동을 추적하여 계산해야 합니다. 이는 라그랑지안 접근법으로 문제를 해결해야 한다는 것을 의미합니다. 러더퍼드 실험에서 충돌 확률을 계산하는 방법과 유사합니다.

실제 우리가 사용하는 챔버의 크기는 cm에서 m 단위입니다. 점성류가 되려면 평균자유거리가 배관 직경의 약 1/100 이어야 하므로, 0.1 mm ~ cm 단위에서 점성류로 취급할 수 있습니다. 예를 들어, 공기의 경우 0℃, 1 atm에서 약 65 nm의 평균자유거리를 가집니다. 이 경우 챔버에 공기를 넣으면 점성류로 간주할 수 있습니다.

그렇다면 공기가 100℃, 1 Torr일 때 평균자유거리는 얼마나 될까요? 평균자유거리는 온도에 비례하고, 압력에 반비례합니다. 온도는 절대온도로 계산해야 하므로, 0℃에서 100℃로 증가하면 약 40% 증가합니다. 압력이 1 atm에서 1 Torr로 감소하면 약 1/760로 감소합니다. 따라서 평균자유거리는 약 1000배 증가하여 60 μm가 됩니다. 이 정도 평균자유거리에서는 약 6 mm까지 점성류 특성을 보일 것입니다.

평균자유거리는 분자 크기의 제곱에 반비례합니다. 비활성 기체, O2, N2 등은 직경이 비슷하므로 평균자유거리도 비슷합니다. 그러나 분자 크기가 큰 분자는 다른 특성을 보일 수 있습니다.

※ 고양이가 직접 쓴 포스트입니다. 

진공은 대기압보다 낮은 상태를 의미하며, 완벽한 진공은 현실적으로 불가능하므로 대기압보다 낮은 상태를 진공이라고 정의합니다. 진공은 수준에 따라 저진공, 중진공, 고진공 등으로 분류됩니다. 대기압에서의 진공은 저진공이나 고진공이나 극고진공 모두 0에 가까워 보이지만, 산업 및 과학 분야에서는 분자의 절대적인 수가 중요합니다.

저진공 이하의 높은 수준의 진공을 사용하는 이유는 힘 외에도 분자의 수 자체가 중요한 특성을 보기 위해서입니다. 예를 들어, 전자빔 용접이나 가속기에서는 입자가 목표한 곳에 정확히 충돌하도록 하기 위해 다른 입자들과의 충돌을 최소화해야 합니다.

이러한 특성은 평균자유거리(Mean Free Path), 충돌빈도(Impingement Rate), 단원자층 형성시간(Monolayer Time) 등으로 나타내며, 설계자는 압력, 분자 종류, 온도에 따른 이러한 특성을 이해하고 있어야 합니다. 이를 통해 라디칼 붕괴, 오염 등의 특성을 유추할 수 있습니다.

진공은 대기압부터 시작해 10의 3제곱 단위로 나누어 분류할 수 있습니다. 이를 통해 각 진공 단위를 쉽게 기억할 수 있습니다. 진공의 단위로는 kPa 외에도 Torr가 많이 사용되며, Torr는 hPa와 비슷한 스케일을 가집니다.

저진공은 일상적인 진공 영역으로, 진공청소기와 같은 음압을 이용한 장치들이 이 영역에 속합니다. 이 영역에서는 압력 스케일이 물체를 움직일 수 있는 힘을 만들어내므로 설계 혹은 동작 시 주의가 필요합니다. 

중진공과 고진공은 반도체, 디스플레이, 광기술 등 표면 반응을 일으키는 설비에 사용됩니다. 이 영역에서는 분자 수에 의한 효과가 중요하며, 최적 압력이 존재합니다. 너무 낮은 압력은 오히려 설비의 목적에 맞지 않을 수 있습니다.

초고진공과 극고진공은 방사광 가속기나 우주항공 분야에서 사용됩니다. 이 레벨에서는 평균자유거리가 매우 길어지고, 분자 간 충돌이 거의 없기 때문에 입자 가속기 등에서 유리합니다.

※ 고양이가 직접 작성한 포스트입니다.